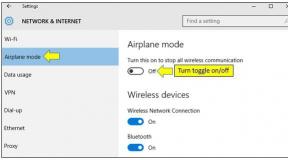
Arhive de etichete: algoritmul lui Dijkstra. Material de curs
Algoritmul lui Dijkstra este conceput pentru a găsi calea cea mai scurtă între vârfuri într-un grafic nedirecționat.
Ideea algoritmului este următoarea: în primul rând, alegem calea către vârful inițial egal cu zero și adăugăm acest vârf la mulțimea celor deja selectate, distanța de la care se determină până la vârfurile rămase neselectate. La fiecare etapă următoare, găsim următorul vârf selectat, distanța la care este cea mai mică, și conectat printr-o muchie de un vârf din mulțimea celor neselectate (această distanță va fi egală cu distanța până la vârful selectat plus lungimea de margine).
Exemplul 1. Găsiți calea cea mai scurtă dintr-un grafic dintr-un vârf L spre vârf D(Fig. 10.7).
Orez. 10.7.
Să scriem algoritmul ca o secvență de pași (Tabelul 10.1). Pas 1. Determinați distanțele de la vârful inițial Lînaintea tuturor.
Tabelul 10.1
Metoda lui Dijkstra (primul pas)
|
Selectat |
Calea către vârful selectat |
Vertex neselectat |
|||||||
Pas 2. Selectați cea mai scurtă distanță de la L la ÎN; vârf găsit ÎN acceptat ca nou selectat. Distanța cea mai mică găsită este adăugată la lungimile muchiilor de la noul vârf ÎNînaintea tuturor. Selectați distanța minimă de la ÎN la N. Vârf nou N acceptat ca selectat (Tabelul 10.2).
Tabelul 10.2
Metoda lui Dijkstra (al doilea pas)
|
Selectat |
Calea către vârful selectat |
Vertex neselectat |
|||||||
Pentru claritate, în viitor, în loc de semnul oo, vom pune semnul „-”.
Pas 3. Determinați distanțele de la vârf N l despre toate cele rămase (cu excepția LŞi ÎN), așa cum se arată în tabel. 10.3.
Tabelul 10.3
Metoda lui Dijkstra (al treilea pas)
|
Selectat |
Calea către vârful selectat |
Vertex neselectat |
|||||||
Distanța de sus L prin vârf N la culmi G este egal cu 18 unități convenționale. Această distanță este mai mare decât distanța LB+BG= 16 unități convenționale, drept urmare nu se ia în considerare în continuare. Continuând construcții similare, alcătuim un tabel. 10.4. Astfel, a fost găsită lungimea celei mai scurte căi dintre vârfuri LŞi D(44 de unități convenționale).
Traiectoria traseului este determinată după cum urmează. Efectuăm o scanare inversă de la vârful final la cel de pornire. Privim prin coloana corespunzătoare vârfului de jos în sus și înregistrăm prima apariție a valorii minime. În coloana corespunzătoare vârfului D, pentru prima dată lungimea minimă de 44 de unități convenționale a apărut în partea de jos în a patra linie. Această linie indică vârful S, spre care să meargă, adică În continuare trebuie să luăm în considerare coloana corespunzătoare vârfului S.
Tabelul 10.4
|
Vârful selectat |
Calea către vârful selectat |
Vertex neselectat |
|||||||
În această coloană, lungimea minimă egală cu 27 de unități convenționale indică următorul vârf G, la care ar trebui să mergi etc. Astfel, obținem traiectoria traseului: (L, B, G, S, D).
Exemplul 8. Găsiți calea cea mai scurtă de pe grafic între vârfurile 1 și 7 (Fig. 10.8).
Determinăm (Tabelul 10.5) următorul vârf selectat, distanța la care este cea mai mică și legată printr-o muchie de unul dintre vârfurile care aparțin mulțimii de vârfuri neselectate (această distanță va fi egală cu distanța până la vârful selectat plus lungimea marginii).

Orez. 10.8. Grafic (O)și matricea de adiacență corespunzătoare (b)
Implementarea tabelară a metodei lui Dijkstra
Tabelul 10.5
|
Selectat |
Calea către vârful selectat |
Vertex neselectat |
||||||
|
la 6 |
||||||||
Efectuăm o scanare inversă de la vârful final la cel de pornire.
Privim prin coloana corespunzătoare vârfului de jos în sus și înregistrăm prima apariție a valorii minime. Cea mai scurtă cale va fi egală cu (V 7 - V 5 - V 2 - U ().
ŞiÎNTREBĂRI DE TEST
- 1. Care este complexitatea teoretică a algoritmilor: construcția arborelui de decizie, programarea dinamică și Dijkstra?
- 2. Care este particularitatea utilizării unui arbore de decizie pentru grafice direcționate și nedirecționate?
- 3. În rezolvarea ce probleme aplicate se folosesc algoritmi pentru a determina cele mai scurte distanțe între vârfurile date dintr-un grafic?
- 4. Poate fi aplicat algoritmul lui Dijkstra discutat în această lucrare la determinarea celei mai scurte distanțe într-un grafic direcționat?
- 5. Cum funcționează algoritmul lui Dijkstra?
- 6. Cum funcționează algoritmul de programare dinamică în raport cu problema determinării celor mai scurte distanțe între vârfuri dintr-un grafic?
Mai întâi, să ne uităm la algoritmul lui Fulkerson (un mod grafic de ordonare a elementelor):
- 1. Găsiți vârfurile graficului care nu includ mai mult de un arc. Ei formează primul grup. Numerotați vârfurile grupului în orice ordine.
- 2. Tăiați toate nodurile și arcurile numerotate care emană din ele. Graficul rezultat conține cel puțin un vârf care nu conține niciun arc. Acestui vârf, inclus în al doilea grup, i se atribuie următorul număr etc. Al doilea pas se repetă până când toate vârfurile sunt ordonate.
Acum luați în considerare un algoritm pentru găsirea celei mai scurte căi dintre două vârfuri date într-un grafic direcționat. Fie G = (S, U, ? ) un grafic direcționat cu arce ponderate. Să notăm vârful s drept începutul căii și vârful t ca sfârșitul căii.
Algoritmul lui Dijkstra conține o limitare - ponderile arcelor trebuie să fie pozitive. Algoritmul în sine constă din două etape. Primul găsește lungimea celui mai scurt drum, al doilea construiește calea în sine de la vârful s la vârful t.
Etapa 1. Găsirea celui mai scurt drum.
Pasul 1. Atribuirea etichetelor inițiale vârfurilor.
Setăm d(s)=0* și considerăm acest semn ca fiind constant (marcajele constante sunt marcate cu un asterisc în partea de sus). Pentru vârfurile rămase x i S, x i ?s setăm d(x i) = ? și considerăm că aceste semne sunt corecte. Fie x” = s, x” desemnarea vârfului curent.
Pasul 2: Schimbați etichetele.
Pentru fiecare vârf x i cu un marcaj temporal imediat după vârful x”, schimbați-i eticheta în conformitate cu următoarea regulă:
d nou (x i) = min(d vechi (x i), d(x”)+ш(x”, x i)).(1. 6. 1)
Pasul 3. Transformarea etichetei din temporară în permanentă.
Din toate nodurile cu marcaje temporale, selectați vârful x j * cu cea mai mică valoare de etichetă
d(x j *) = min (d(x j) / x j S, d(x j) - temporar). (1. 6. 2)
Transformăm acest semn într-o constantă și setăm x” = x j *.
Pasul 4. Verificați finalizarea primei etape.
Dacă x” = t, atunci d(x”) este lungimea celei mai scurte căi de la s la t. În caz contrar, revenim la a doua etapă.
Etapa 2. Construirea căii celei mai scurte.
Pasul 5. Căutare secvenţială pentru arce de calea cea mai scurtă.
Printre vârfurile imediat precedând vârful x” cu etichete constante, găsim un vârf x i care satisface relația
d(x”) = d(x i) + u(x i, x”).(1. 6. 3)
Includem arcul (x i, x”) în calea dorită și setăm x” = x i.
Pasul 6. Verificați finalizarea celei de-a doua etape.
Dacă x” = s, atunci s-a găsit calea cea mai scurtă - este formată dintr-o succesiune de arce obținute la pasul a cincea și dispuse în ordine inversă. În caz contrar, revenim la a cincea etapă.
Exemplul 8: Matricea de ponderi dată? graficul G. Găsiți calea minimă de la vârful x 1 la vârful x6 folosind algoritmul lui Dijkstra.

Figura 1.11 prezintă graficul în sine bazat pe această matrice de greutate. Deoarece acest grafic are un ciclu între vârfurile x 2 , x 3 și x 5 , vârfurile graficului nu pot fi ordonate folosind algoritmul Fulkerson. În figura grafică, etichetele temporare și permanente sunt indicate deasupra vârfului corespunzător. Deci, să descriem în detaliu funcționarea algoritmului lui Dijkstra pas cu pas.
Pasul 1. Setați d(x 1) = 0*, x” = x 1, d(x 2) = d(x 3) = d(x 4) = d(x 5) = d(x 6) = ? .
Prima iterație.
Pasul 2. Set de vârfuri imediat după x” = x1 cu marcaje temporale S” = (x 2 , x 4 , x 5 ). Recalculăm marcajele de timp ale vârfurilor: d(x 2) = min(?, 0*, + 9) = 9, d(x 4) = min(?, 0* + 6) = 6, d(x 5) = min(?, 0* + 11) = 11.
Pasul 3. Unul dintre marcajele temporale se transformă într-o constantă min(9, ?, 6, 11, ?) = 6* = d(x 4), x” = x 4.
Pasul 4. x” = x 4 ? t = x 6 , există o întoarcere la a doua etapă.
a 2-a iterație.
Pasul 2. S” = (x 2, x 3, x 5), d(x 2) = min(9, 6* + 5) = 9, d(x 3) = min (?, 6* + 7) = 13, d(x 5) = min(11, 6* + 6) = 11.
Pasul 3. min(d(x 2), d(x 3), d(x 5), d(x 6)) = min(9, 13, 11, ?) = 9* = d(x 2), x” = x2.
Pasul 4. x 2 ? x 6 , reveniți la pasul al doilea.
A 3-a iterație.
Pasul 2. S” =(x 3 ), d(x 3) = min(13, 9* + 8) = 13.
Pasul 3. min(d(x 3), d(x 5), d(x 6)) = min(31, 11, ?) = 11* = d(x 5), x” = x 5.
Pasul 4. x 5 ? x 6 , reveniți la pasul al doilea.
A 4-a iterație.
Pasul 2. S”=(x 6), d(x 6) = min(?, 11* + 4) = 15.
Pasul 3. min (d(x 3), d(x 6)) = min(13, 15) = 13* = d(x 3), x” = x 3.
Pasul 4. x 3 ? x 6 , reveniți la pasul al doilea.
A 5-a iterație.
Pasul 2. S” = (x 6 ), d(x 6) = min(15, 13* + 9) = 15.
Pasul 3. min(d(x 6) ) = min(15) = 15*, x” = x 6 .
Pasul 4. x 6 = t = x 6, sfârșitul primei etape.
Pasul 5. Să creăm un set de vârfuri imediat precedând x” = x 6 cu etichete constante S” = (x 3, x 5). Să verificăm pentru aceste două vârfuri dacă egalitatea d este nouă. (x i) = min(d vechi (x i), d(x”) + w(x”, x i)):
d(x”) = 15 = 11* + 4 = d(x 5) + u(x 5, x 6),
d(x”) = 15 ? 13* + 9 = d(x 3) + u(x 3, x 6).
Includem arcul (x 5 , x 6) în calea cea mai scurtă. x” = x 5 .
Pasul 6. x” ? s = x 1 , reveniți la pasul a cincea.
a 2-a iterație.
Pasul 5. S” = (x 1, x 4).
d(x”) = 11 = 0* + 11 = d(x 1) + u(x 1, x 5),
d(x”) = 11 ? 6* + 6 = d(x 4) + u(x 4, x 5).
Includem arcul (x 1 , x 5) în calea cea mai scurtă. x” = x 1 .
Pasul 6. x” = s = x 1, finalizarea celei de-a doua etape.
Deci, calea cea mai scurtă de la vârful x 1 la vârful x 6 a fost construită. Lungimea (greutatea) sa este de 15, calea în sine este formată din următoarea succesiune de arce: m = (x 1, x 5) - (x 5, x 6).
La finalul turneului de Revelion, sponsorul a decis să trimită $m$ cadouri câștigătorilor prin poștă. Cunoscând numărul de participanți $n$ și timpul de livrare a corespondenței dintre unele filiale Ukrposhta, găsiți timpul minim după care ultimul câștigător își va primi premiul.
Date de intrare
Prima linie conține numere de $3$: numărul de participanți la turneu $n$, numărul de premii pentru sponsor $m$ și numărul de timpi de livrare cunoscuți între unele dintre ramuri $k$. Rândul următor conține numerele participanților care au devenit câștigători, separate printr-un spațiu.
Urmează $k$ linii de $3$ numere fiecare cu informații despre timpii de livrare cunoscuți între unele ramuri în formatul: $a$ $b$ $t$, unde $a$ și $b$ sunt numere de departament, $t $ $(0 \leqslant t \leqslant 365)$ — timpul de livrare a corespondenței între ei. Ultimul rând conține un singur număr - numărul oficiului poștal de la care sponsorul va trimite premiile. Se știe că $1 \leqslant n, m, a, b \leqslant 365$.
Imprima
Dacă toate premiile sunt livrate participanților, tipăriți „Sponsorul bun!” pe prima linie, iar în rândul următoare timpul după care ultimul câștigător își va primi premiul. Dacă cel puțin unul dintre participanți nu reușește să primească premiul, tipăriți „Nu este vina sponsorului...” pe un singur rând. Exprimați fraze fără ghilimele.
Teste
| № | Date de intrare | Imprima |
| 1. | 3 2 2 2 3 1 2 3 2 3 4 1 |
Sponsorul bun! 7 |
| 2. | 5 1 4 5 1 3 2 2 3 3 4 2 5 4 5 6 1 |
Sponsorul bun! 16 |
| 3. | 7 2 6 1 3 1 3 2 2 4 32 4 5 94 3 1 0 6 2 4 7 2 3 7 |
Nu este vina sponsorului... |
| 4. | 5 2 6 1 2 3 1 1 3 4 2 2 4 3 5 1 4 4 5 5 2 3 7 2 |
Sponsorul bun! 6 |
Rezolvați problema găsirii celei mai scurte căi folosind algoritmul lui Dijkstra.
Găsiți cea mai scurtă cale de la X0 la X7. Graficul este definit de elementele matricei costurilor
Să construim acest grafic 
Să începem cu elementul X0 și să îi atribuim eticheta 0, luând în considerare toți vecinii săi, deoarece Nu există încă semne acolo, apoi le vom atribui lungimile corespunzătoare: 
Toți vecinii lui X0 au fost luați în considerare, marcați-l și treceți la vârful X1. Vecinii lui sunt X0, X2, X4, dar X0 este marcat, nu îl luăm în considerare. Pentru X2: ![]() , lasa un semn.
, lasa un semn.
Pentru X4: ![]() , înlocuiți eticheta. Toți vecinii vârfului X1 au fost luați în considerare, marcați-l
, înlocuiți eticheta. Toți vecinii vârfului X1 au fost luați în considerare, marcați-l 
mergeți în partea de sus X2. Vecinii ITS X0, X1, X3, X4, X5, X6, dar X0, X1 sunt marcați, nu le luăm în considerare.
Pentru X3: ![]() , lasa un semn.
, lasa un semn.
Pentru X5: ![]() , înlocuiți eticheta.
, înlocuiți eticheta.
Pentru X4: ![]() , lasa un semn.
, lasa un semn.
Pentru X6: ![]() , înlocuiți eticheta.
, înlocuiți eticheta.
Toți vecinii vârfului X2 au fost luați în considerare, așa că îl marchem. 
trecem în vârful lui X3. Vecinii ITS X0, X2, X6, dar X0, X2 sunt marcați, nu le luăm în considerare.
Pentru X6: ![]() , lasa un semn.
, lasa un semn.
Toți vecinii vârfului X3 au fost luați în considerare, așa că îl marchem. 
trecem în vârful lui X4. Vecinii ITS X1, X2, X5, X7, dar X1, X2 sunt marcați, nu le luăm în considerare.
Pentru X5: ![]() , înlocuiți eticheta.
, înlocuiți eticheta.
Pentru X7: ![]() , înlocuiți eticheta.
, înlocuiți eticheta.
Toți vecinii vârfului X4 au fost luați în considerare, așa că îl marchem. 
trecem în vârful lui X5. Vecinii ITS X2, X4, X6, X7, dar X2, X4 sunt marcați, nu le luăm în considerare.
Pentru X6: ![]() , lasa un semn.
, lasa un semn.
Pentru X7: ![]() , lasa un semn.
, lasa un semn.
Toți vecinii vârfului X5 au fost luați în considerare, așa că îl marchem. 
mergeți sus X6. Vecinii ITS X2, X3, X5, X7, dar X2, X3, X5 sunt marcați, nu îi luăm în considerare.
Pentru X7: ![]() , lasa un semn.
, lasa un semn.
Toți vecinii vârfului X6 au fost luați în considerare, așa că îl marchem. Și marchem X7 rămas, toate nodurile au fost luate în considerare. 
Concluzie: Cea mai scurtă cale de la X0 la X7 are o lungime de 101, această cale: X7-X4-X1-X0.
Algoritmul lui Dijkstra este un algoritm grafic care găsește calea cea mai scurtă între două vârfuri date într-un grafic cu lungimi de arc nenegative. Sarcina de a calcula calea cea mai scurtă de la un punct dat la toate celelalte este, de asemenea, pusă adesea. Algoritmul este utilizat pe scară largă în programare, de exemplu, este folosit în protocoalele de rutare.
Descriere
Intrarea algoritmului este un grafic direcționat ponderat cu arce de greutate nenegativă. Ieșirea este un set de cele mai scurte căi de la un punct dat la alții.
La început, se presupune că distanța pentru vârful inițial este zero, iar distanța față de toate celelalte se presupune a fi infinite. O matrice de steaguri care indică dacă vârful a fost trecut este umplută cu zerouri. Apoi, la fiecare pas al ciclului, se caută un vârf cu o distanță minimă față de cel inițial și un steag egal cu zero. Este setat un steag pentru acesta și toate nodurile învecinate sunt verificate. Dacă distanța calculată anterior de la vârful inițial la cel care se verifică este mai mare decât suma distanței până la vârful curent și lungimea muchiei de la acesta până la vârful verificat, atunci distanța până la vârful verificat este egalată. la distanța până la curent + muchie de la curent la cel care se verifică. Ciclul se termină când steagurile tuturor nodurilor devin egale cu 1 sau când distanța până la toate nodurile cu un steag 0 este infinită. Ultimul caz este posibil dacă și numai dacă graficul este deconectat.
algoritmul lui Dijkstra în pseudocod
Intrare: CU: matrice de real – matricea lungimii arcului grafic; s este vârful de la care se caută calea cea mai scurtă și t este vârful către care se caută.
Ieșire: vectori T: matrice de real; și N: matrice de 0..r. Dacă vârful v se află pe calea cea mai scurtă de la s La t, Că Televizor]- lungimea celui mai scurt drum de la s La y; Ei bine] - vârful imediat precedent la pe calea cea mai scurtă.
Н – un tablou în care vârful n corespunde vârfului m, cel anterior în drum spre n de la s.
T este un tablou în care vârful n corespunde distanței de la acesta la s.
X este o matrice în care vârful n corespunde cu 1 dacă calea către acesta este cunoscută și 0 dacă nu.
inițializarea matricelor:
pentru v de la 1 la r do
T[v]: = ∞ (cea mai scurtă cale necunoscută)
X[v]: = 0 (toate vârfurile sunt nemarcate)
H[s]: = 0 ( s nimic nu precede)
T[s]: = 0 (cea mai scurtă cale are lungimea 0...)
X[s]: = 1 (...si el este celebru) v : = s (top actual)
M: (note de actualizare)
pentru și ∈ G( Şi) face
dacă X[i] = 0 & T[i]> Televizor] + C apoi
T[i]: = Televizor] + C(am găsit un traseu mai scurt de la s V Şi prin v }
H[u]:= v(ține minte)
m: = ∞
v : = 0
(găsește capătul celui mai scurt drum)
pentru Şi de la 1 la p do
dacă X[u] = 0 &T[u]< t apoi
v:= u;
m:= T[u](top v termină calea cea mai scurtă de la s
dacă v = 0 atunci
oprire (nici o cale de la s V t) termina dacă
dacă v= t apoi
stop (a găsit cea mai scurtă cale de la s V t) termina dacă
X[v]: = 1 (a găsit cea mai scurtă cale de la s V v ) du-te la M
Motivație
Pentru a demonstra corectitudinea algoritmului lui Dijkstra, este suficient să rețineți că de fiecare dată când corpul buclei care începe cu eticheta M este executat, v se folosește un vârf pentru care se cunoaște calea cea mai scurtă de la vârf s. Cu alte cuvinte, dacă X[v] = 1, atunci T[v] = d(s,v) , iar toate vârfurile de pe calea (s,v) definită de vectorul H au aceeași proprietate, adică
Vu T[u] = 1 => T[u] = d(s,u)&T] = 1.
Într-adevăr (prin inducție), prima dată ca v se folosește un vârf s pentru care calea cea mai scurtă este goală și are lungimea 0 (căile nevide nu pot fi mai scurte deoarece lungimile arcurilor sunt nenegative). Fie T[u] = d(s,u) pentru toate nodurile marcate anterior Şi. Luați în considerare noul vârf etichetat v, care este selectat din condiția T[v] = min T[i]. Rețineți că dacă calea care trece prin vârfurile marcate este cunoscută, atunci calea cea mai scurtă este cunoscută. Să presupunem (prin contradicție) că T[v]> d(s, v), adică calea găsită care duce de la s V v, nu este cel mai scurt. Atunci trebuie să existe vârfuri nemarcate pe această cale. Luați în considerare primul vârf w pe această cale, astfel încât T[w] = 0.Avem: T[w] = d(s,w)⩽d(s>v)< Т[v],что противоречит выбору вершины u.
Complexitatea timpului
Complexitatea algoritmului lui Dijkstra depinde de metoda de găsire a unui vârf nevizitat cu distanța minimă față de cel original, de metoda de stocare a setului de vârfuri nevizitate și de metoda de actualizare a etichetelor. Fie n numărul de vârfuri, iar m numărul de muchii din grafic. Apoi, în cel mai simplu caz, atunci când întregul set de vârfuri este căutat pentru a găsi un vârf cu distanța minimă până la vârful inițial și se folosește o matrice pentru a stoca distanțele, timpul de rulare al algoritmului este O(n 2). Bucla principală este executată de aproximativ n ori, în fiecare dintre ele se cheltuiesc aproximativ n operații pentru găsirea minimului. Ciclurile prin vecinii fiecărui vârf vizitat necesită un număr de operații proporțional cu numărul de muchii m (deoarece fiecare muchie are loc exact de două ori în aceste cicluri și necesită un număr constant de operații). Astfel, timpul total de rulare al algoritmului este O(n 2 +m), dar întrucât m este mult mai mic decât n(n-1), rezultatul final este O(n 2).
Pentru graficele rare (adică cele pentru care m este mult mai mic decât n²), vârfurile nevizitate pot fi stocate în heap-ul binar, iar valorile distanței pot fi folosite ca cheie. Deoarece bucla este executată de aproximativ n ori, iar numărul de relaxări (modificări de etichetă) nu este mai mare de m, timpul de rulare al unei astfel de implementări este O(nlogn+mlogn)
Exemplu
Calculul distanțelor de la vârful 1 pe baza vârfurilor traversabile: