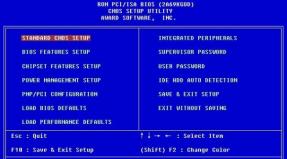
Дискретные и непрерывные модели. Статические и динамические, дискретные и непрерывные модели Трехмерное изменение масштаба
Система может быть дискретной или непрерывной по входам, по выходам и по времени в зависимости от того, дискретными или непрерывными являются множества U, У, Т соответственно. Под дискретным понимается конечное или счетное множество. Под непрерывным будем понимать множество объектов, для которого адекватной моделью служит отрезок, луч или прямая линия, т. е. связное числовое множество. Если система имеет несколько входов и выходов, то это значит, что соответствующие множества U, Т лежат в многомерных пространствах, т. е. непрерывность и дискретность понимаются покомпонентно.
Удобство числового множества как модели реальных совокупностей объектов состоит в том, что на нем естественным образом определяются несколько отношений, формализующих реально встречающиеся отношения между реальными объектами. Например, отношения близости, сходимости формализуют понятия похожести, сходства объектов и могут быть заданы посредством функции расстояния (метрики) d(x, у) (например, d(x, y)= Іx-y І. Числовые множества являются упорядоченными: отношение порядка следования (х у) формализует предпочтение одного объекта другому. Наконец, над элементами числовых множеств определены естественные операции, например, линейные: х+у, х-у. Если для реальных объектов на входе и выходе также имеют смысл аналогичные операции, то естественным образом возникают требования к моделям (2.1) -(2.3): быть согласованными с этими операциями, сохранять их результаты. Так мы приходим, например, к линейным моделям: , du/dt = ay + bu и т.д., являющимся простейшими моделями многих процессов.
Как правило, дискретность множества U влечет за собой дискретность Y . Кроме того, для статических систем исчезает разница между непрерывным и дискретным временем. Поэтому классификация детерминированных систем по признакам «статические - динамические», «дискретные - непрерывные» включает шесть основных групп, представленных в табл. 1.3, где для каждой группы указан математический аппарат описания систем, методы численного анализа и оценки их параметров, методы синтеза (оптимизации), а также типичные области применения.
Пример 1. Рассмотрим работу турникета на входе в метро. В первом, «грубом» приближении множество значений входа этой системы имеет два элемента: человек с жетоном (u 1) и человек без жетона , т.е. U={ u 1 }. После небольшого размышления становится ясно, что следует включить еще отсутствие пассажира (u 0), т.е. U ={u 0 , u 1 , }. Множество значений выхода содержит элементы «открыто» (y 0) и «закрыто» (y 1). Таким образом, Y={y 0 , y 1 } и система является дискретной. В простейшем случае можно пренебречь памятью системы и описывать ее статической моделью, имеющей вид таблицы или графа:
При необходимости хранить ММ системы в ЭВМ ее можно представить (закодировать) в виде матрицы или более экономно, в виде списка (0, 0, 1), в котором на i -м месте стоит j , если значению входа соответствует значение выхода y i .
Пример 2. Если нас интересует более детально устройство самого турникета (т.е. системой является турникет), то придется учесть, что входными воздействиями (сигналами) для него являются опускание пятака и прохождение человека через турникет. Таким образом, система имеет два входа, каждый из которых может принимать два значения («есть» или «нет»).
Пренебрегая возможностью одновременного опускания жетона и прохождения, вводим три значения входа: и
0 - «нет воздействия», и
1 - «опускание жетона», и
2 - «прохождение». Множество Y
можно задать так же, как и в примере 1. Однако теперь значение выхода y
(t
)не определяется только значением входа и
(t
),а зависит еще и оттого, был ли опущен жетон раньше, т.е. от значений u(s)
при s
x (k+1)=F (x(k), и (k)), y (k) = G (x(k), и (к)), (2.4]
где k - номер момента времени такта. Отметим, что, выделив «текущий» и «следующий» моменты времени, мы незаметно ввели предположение о дискретности времени, которое при более детальном исследовании может оказаться неправомерным см. ниже п. 2.2.3). Функцию переходов F (х, и)и функцию выходов G (x, и )можно задать таблично:
Можно также построить графы переходов и выходов:
Пример 3. Рассмотрим простейшую электрическую цепь - RС -цепочку (рис. 1.6). Входом системы является напряжение источника u(t )=E 0 (t ), выходом - напряжение на конденсаторе y (t )=E 1 (t ). Закон Ома дает ММ системы в виде дифференциального уравнения 1-го порядка
у=и - у ,(2.5)
где -RC - постоянная времени цепочки. ММ (2.5) полностью непрерывна: U==Y=T=R 1 . Если исследователя интересует поведение системы в статических режимах, т.е. при E 0 (t )= const, то нужно положить в (2.5) у= 0и получить статическую модель
y (t )=u (t ).(2.6)
Моделью (2.6) можно пользоваться как приближенной в I случае, когда вход E 0 (t )изменяется достаточно редко или медленно (по сравнению с ).
Пример 4. Рассмотрим экологическую систему, состоящую из двух взаимодействующих популяций ,существующих на некоторой территории. Предположим, что система автономна, т.е. внешними воздействиями (входами) можно пренебречь; за выходы системы примем численности популяций (видов) y 1 (t ), y 2 (t ). Пусть 2-й вид является пищей для 1-го, т.е. система относится к классу «хищник - жертва» (например, у 1 - численность лис в лесу, а у 2 - численность зайцев; или у 1 - концентрация бактерий-возбудителей заболевания в городе, а у 2 - число заболевших и т.д.). В данном случае у 1 , у 2 - целые числа и, на первый взгляд, в ММ системы множество Y должно быть дискретным. Однако для построения ММ удобнее считать, что у 1 , у 2 могут принимать произвольные вещественные значения, т.е. перейти к непрерывной модели (при достаточно больших у 1 , у 2 этот переход не внесет существенной погрешности). При этом мы сможем пользоваться такими понятиями, как скорости изменения выходных переменных у 1 , у 2 . Простейшая модель динамики популяции получается, если предположить, что:
При отсутствии хищников численность жертв растет экспоненциально;
При отсутствии жертв численность хищников убывает экспоненциально;
Численность «съеденных» жертв пропорциональна величине у 1 , у 2 .
При этих предположениях динамика системы, как нетрудно видеть, описывается так называемой моделью Лотки - Вольтерра:
где а, Ь, с, d - положительные параметры. Если есть возможность изменять параметры, то они превращаются во входные переменные, например, когда изменяются коэффициенты рождаемости и смертности видов, коэффициенты размножения бактерий (при введении лекарств) и т.д.
Пример.
Пример.
Пример.
Пример. Модель S=gt2/2, 0 < t < 100 непрерывна на промежутке времени (0;100).
Пример.
a1x1 + a2x2 = S,
Детерминированные и стохастические модели
Модель детерминированная, если каждому входному набору параметров соответствует вполне определенный и однозначно определяемый набор выходных параметров; в противном случае - модель недетерминированная, стохастическая (вероятностная).
Пример. Приведенные выше физические модели - детерминированные. Если в модели S = gt2 / 2, 0 < t < 100 мы учли бы случайный параметр - порыв ветра с силой p при падении тела:
S(p) = g(p) t2 / 2, 0 < t < 100,
то мы получили бы стохастическую модель (уже не свободного) падения.
Функциональные, теоретико-множественные и логические модели
Модель функциональная, если она представима в виде системы каких- либо функциональных соотношений.
Модель теоретико-множественная, если она представима с помощью некоторых множеств и отношений принадлежности им и между ними.
Пример. Пусть задано множество
X = {Николай, Петр, Николаев, Петров, Елена, Екатерина, Михаил, Татьяна} и отношения:
Николай - супруг Елены,
Екатерина - супруга Петра,
Татьяна - дочь Николая и Елены,
Михаил - сын Петра и Екатерины,
семьи Михаила и Петра дружат друг с другом.
Тогда множество X и множество перечисленных отношений Y могут служить теоретико-множественной моделью двух дружественных семей.
Модель называется логической, если она представима предикатами, логическими функциями.
Например, совокупность логических функций вида:
z = x y x, p = x y
есть математическая логическая модель работы дискретного устройства.
Игровые модели
Модель игровая, если она описывает, реализует некоторую игровую ситуацию между участниками игры.
Пример. Пусть игрок 1 - добросовестный налоговый инспектор, а игрок 2 - недобросовестный налогоплательщик. Идет процесс (игра) по уклонению от налогов (с одной стороны) и по выявлению сокрытия уплаты налогов (с другой стороны). Игроки выбирают натуральные числа i и j (i, j n), которые можно отождествить, соответственно, со штрафом игрока 2 за неуплату налогов при обнаружении игроком 1 факта неуплаты и с временной выгодой игрока 2 от сокрытия налогов. Если в качестве модели взять матричную игру с матрицей выигрышей порядка n, то в ней каждый элемент определяется по правилу aij = |i - j|. Модель игры описывается этой матрицей и стратегией уклонения и поимки. Эта игра - антагонистическая.
Лингвистические модели
Модель называется языковой, лингвистической, если она представлена некоторым лингвистическим объектом, формализованной языковой системой или структурой.
Иногда такие модели называют вербальными, синтаксическими.
Например, правила дорожного движения - языковая, структурная модель движения транспорта и пешеходов на дорогах.
Пусть B - множество производящих основ существительных, C - множество суффиксов, P - прилагательных, b i – корень слова; "+" - операция конкатенации слов, ":=" - операция присваивания, "=>" - операция вывода (выводимости новых слов), Z - множество значений (смысловых) прилагательных.
Языковая модель M словообразования может быть представлена:
= + <с i >.
При b i - "рыб(а)", с i - "н(ый)", получаем по этой модели p i - "рыбный", z i - "приготовленный из рыбы".
Система клеточных автоматов
Модель клеточно-автоматная, если она представима клеточным автоматом или системой клеточных автоматов.
Клеточный автомат - дискретная динамическая система, аналог физического (непрерывного) поля. Клеточно-автоматная геометрия - аналог евклидовой геометрии. Неделимый элемент евклидовой геометрии - точка, на основе ее строятся отрезки, прямые, плоскости и т.д.
Неделимый элемент клеточно-автоматного поля - клетка, на основе её строятся кластеры клеток и различные конфигурации клеточных структур. Представляется клеточный автомат равномерной сетью клеток ("ячеек") этого поля. Эволюция клеточного автомата разворачивается в дискретном пространстве - клеточном поле.
Смена состояний в клеточно-автоматном поле происходит одновременно и параллельно, а время идет дискретно. Несмотря на кажущуюся простоту их построения, клеточные автоматы могут демонстрировать разнообразное и сложное поведение объектов, систем.
В последнее время они широко используются при моделировании не только физических, но и социально-экономических процессов.
Фрактальные модели
Модель называется фрактальной, если она описывает эволюцию моделируемой системы эволюцией фрактальных объектов.
Если физический объект однородный (сплошной), т.е. в нем нет полостей, то можно считать, что его плотность не зависит от размера. Например, при увеличении параметра объекта R до 2R масса объекта увеличится в R 2 раз, если объект- круг и в R 3 раз, если объект - шар, т.е. существует связь массы и длины. Пусть n - размерность пространства. Объект, у которого масса и размер связаны называется "компактным". Его плотность можно рассчитать по формуле:
![]()
Если объект (система) удовлетворяет соотношению M(R) ~ R f(n) , где f(n) < n, то такой объект называется фрактальным.
Его плотность не будет одинаковой для всех значений R, то она масштабируется согласно формуле:
![]()
Так как f(n) - n < 0 по определению, то плотность фрактального объекта уменьшается с увеличением размера R, а ρ(R) является количественной мерой разряженности объекта.
Пример фрактальной модели - множество Кантора. Рассмотрим отрезок . Разделим его на 3 части и выбросим средний отрезок. Оставшиеся 2 промежутка опять разделим на три части и выкинем средние промежутки и т.д. Получим множество, называемое множеством Кантора. В пределе получаем несчетное множество изолированных точек (рис. 1.4 )
Рис. 1.4. Множество Кантора для 3-х делений
Генетические алгоритмы
Идея генетических алгоритмов "подсмотрена" у систем живой природы, у которых эволюция развертывается достаточно быстро.
Генетический алгоритм - это алгоритм, основанный на имитации генетических процедур развития популяции в соответствии с принципами эволюционной динамики.
Генетические алгоритмы используются для решения задач оптимизации (многокритериальной), для задач поиска и управления.
Данные алгоритмы адаптивны, они развивают решения и развиваются сами.
Генетический алгоритм может быть построен на основе следующей укрупненной процедуры:.
Хотя генетические алгоритмы и могут быть использованы для решения задач, которые, нельзя решить другими методами, они не гарантируют нахождение оптимального решения, по крайней мере, за приемлемое время. Здесь более уместны критерии типа "достаточно хорошо и достаточно быстро".
Главное же преимущество их использования заключается в том, что они позволяют решать сложные задачи, для которых не разработаны пока устойчивые и приемлемые методы, особенно на этапе формализации и структурирования системы.
Генетические алгоритмы эффективны в комбинации с другими классическими алгоритмами и эвристическими процедурами.
Статические и динамические, дискретные и непрерывные модели
Классификацию моделей проводят по различным критериям.
Модель называется статической, если среди параметров, участвующих в ее описании, нет временного параметра. Статическая модель в каждый момент времени дает лишь "фотографию" системы, ее срез.
Пример. Закон Ньютона F=a*m - это статическая модель движущейся с ускорением a материальной точки массой m. Эта модель не учитывает изменение ускорения от одной точки к другой.
Модель динамическая, если среди ее параметров есть временной параметр, т.е. она отображает систему (процессы в системе) во времени.
Пример. Динамическая модель закона Ньютона будет иметь вид:
Модель дискретная, если она описывает поведение системы только в дискретные моменты времени.
Пример. Если рассматривать только t=0, 1, 2, …, 10 (сек), то модель
или числовая последовательность: S0=0, S1=g/2, S2=2g, S3=9g/2, :, S10=50g может служить дискретной моделью движения свободно падающего тела.
Модель непрерывная, если она описывает поведение системы для всех моментов времени некоторого промежутка времени.
Пример. Модель S=gt2/2, 0 < t < 100 непрерывна на промежутке времени (0;100).
Модель имитационная, если она предназначена для испытания или изучения возможных путей развития и поведения объекта путем варьирования некоторых или всех параметров модели.
Пример. Пусть модель экономической системы производства товаров двух видов 1 и 2, в количестве x1 и x2 единиц и стоимостью каждой единицы товара a1 и a2 на предприятии описана в виде соотношения:
a1x1 + a2x2 = S,
где S - общая стоимость произведенной предприятием всей продукции (вида 1 и 2). Можно ее использовать в качестве имитационной модели, по которой можно определять (варьировать) общую стоимость S в зависимости от тех или иных значений объемов и стоимости производимых товаров.
Реальные физические объекты функционируют в непрерывном времени, и для изучения многих проблем физических систем их модели должны быть непрерывными . Состояние таких моделей изменяется непрерывно во времени. Это модели движения в реальных координатах, модели химического производства и т. п. Процессы движения объектов и процессы перекачки нефти в модели нефтеналивного порта являются непрерывными.
На более высоком уровне абстракции для многих систем адекватными являются модели, в которых переходы системы из одного состояния в другое можно считать мгновенными, происходящими в дискретные моменты времени. Такие системы называются дискретными . Примером мгновенного перехода является изменение числа клиентов банка или количества покупателей в магазине. Очевидно, что дискретные системы - это абстракция, процессы в природе не происходят мгновенно. В реальный магазин реальный покупатель входит в течение некоторого времени, он может застрять в дверях, колеблясь, войти или нет, и всегда существует непрерывная последовательность его положения во время прохождения дверей магазина. Однако при построении модели магазина для оценки, например, средней длины очереди в кассу при заданном потоке покупателей и известных характеристиках обслуживания кассиром клиентов можно абстрагироваться от этих второстепенных явлений и считать систему дискретной: результаты анализа полученной дискретной модели обычно достаточно точны для принятия обоснованных управленческих решений для подобных систем. В модели нефтеналивного порта мгновенными можно считать, например, переходы светофоров на входе в гавань из состояния "запрещено" в состояние "разрешено". На еще более высоком уровне абстракции при анализе систем также используются непрерывные модели, что характерно для системной динамики. Потоки машин на автострадах, потребительский спрос, распространение инфекции среди населения часто удобно описывать с помощью взаимозависимостей непрерывных переменных, описывающих количества, интенсивности изменения этих количеств, степени влияния одних количеств на другие. Соотношения таких переменных выражаются обычно дифференциальными уравнениями.
Во многих случаях в реальных системах присутствуют оба типа процессов, и если оба они являются существенными для анализа системы, то и в модели одни процессы должны представляться как непрерывные, другие - как дискретные. Такие модели со смешанным типом процессов называются гибридными. Например, если при анализе функционирования магазина существенным является не только количество покупателей, но и пространственное их положение и перемещение покупателей, то модель в этом случае должна представлять смесь непрерывных и дискретных процессов, т. е. это гибридная модель. Другим примером может служить модель функционирования крупного банка. Поток инвестиций, получение и выдача кредитов в нормальном режиме описывается набором дифференциальных и алгебраических уравнений, т. е. модель является непрерывной. Однако существуют ситуации, например дефолт (дискретное событие), в результате чего возникает паника у населения, и с этого момента система описывается совершенно другой непрерывной моделью. Модель данного процесса на том уровне абстракции, на котором мы хотим адекватно описать оба режима работы банка и переход между режимами, должна включать как описание непрерывных процессов, так и дискретные события, а также их взаимозависимости.
Пакет AnyLogic поддерживает описание как непрерывных, так и дискретных процессов, а также строить гибридные модели.. AnyLogic позволяет реализовать модель, фактически, на любом уровне абстракции (детальности). Выполнение гибридных моделей в AnyLogic основано на современных результатах теории гибридных динамических систем.
Аннотация: Первая тема имеет вводный, в основном, терминологический характер. Подробно раскрываются понятия модели и моделирования, их назначение как основного, а подчас, и единственного метода анализа и синтеза сложных систем и процессов. Дается обзор классификации моделей и моделирования, в некоторой мере упрощенный, но достаточный для полного уяснения сущности моделирования как вообще, так и математического в частности.
Сам по себе процесс моделирования в полной мере не формализован, большая роль в этом принадлежит опыту инженера. Но, тем не менее, рассматриваемый в теме процесс создания модели в виде шести этапов может стать основой для начинающих и с накоплением опыта может быть индивидуализирован.
Математическая модель , являясь абстрактным образом моделируемого объекта или процесса, не может быть его полным аналогом. Достаточно сходства в тех элементах, которые определяют цель исследования. Для качественной оценки сходства вводится понятие адекватности модели объекту и, в связи с этим, раскрываются понятия изоморфизма и изофункционализма. Формальных приемов, позволяющих автоматически, "бездумно", создавать адекватные математические модели, нет. Окончательное суждение об адекватности модели дает практика, то есть сопоставление модели с действующим объектом. И, тем не менее, усвоение всех последующих тем пособия позволит инженеру справляться с проблемой обеспечения адекватности моделей.
Завершается тема изложением требований к моделям, которые были сформулированы Р. Шенноном на заре компьютерного моделирования тридцать лет назад в книге " Имитационное моделирование систем - искусство и наука". Актуальность этих требований сохраняется и в настоящее время.
1.1. Общее определение модели
Практика свидетельствует: самое лучшее средство для определения свойств объекта - натурный эксперимент , т. е. исследование свойств и поведения самого объекта в нужных условиях. Дело в том, что при проектировании невозможно учесть многие факторы, расчет ведется по усредненным справочным данным, используются новые, недостаточно проверенные элементы (прогресс нетерпелив!), меняются условия внешней среды и многое другое. Поэтому натурный эксперимент - необходимое звено исследования. Неточность расчетов компенсируется увеличением объема натурных экспериментов, созданием ряда опытных образцов и "доводкой" изделия до нужного состояния. Так поступали и поступают при создании, например, телевизора или радиостанции нового образца.
Однако во многих случаях натурный эксперимент невозможен.
Например, наиболее полную оценку новому виду вооружения и способам его применения может дать война. Но не будет ли это слишком поздно?
Натурный эксперимент с новой конструкцией самолета может вызвать гибель экипажа.
Натурное исследование нового лекарства опасно для жизни человека.
Натурный эксперимент с элементами космических станций также может вызвать гибель людей.
Время подготовки натурного эксперимента и проведение мероприятий по обеспечению безопасности часто значительно превосходят время самого эксперимента. Многие испытания, близкие к граничным условиям, могут протекать настолько бурно, что возможны аварии и разрушения части или всего объекта.
Из сказанного следует, что натурный эксперимент необходим, но в то же время невозможен либо нецелесообразен.
Выход из этого противоречия есть и называется он " моделирование ".
Моделирование - это замещение одного объекта другим с целью получения информации о важнейших свойствах объекта-оригинала.
Отсюда следует.
Моделирование - это, во-первых, процесс создания или отыскания в природе объекта, который в некотором смысле может заменить исследуемый объект . Этот промежуточный объект называется моделью . Модель может быть материальным объектом той же или иной природы по отношению к изучаемому объекту (оригиналу). Модель может быть мысленным объектом, воспроизводящим оригинал логическими построениями или математическими формулами и компьютерными программами.
Моделирование , во-вторых, это испытание , исследование модели. То есть, моделирование связано с экспериментом, отличающимся от натурного тем, что в процесс познания включается "промежуточное звено" - модель. Следовательно, модель является одновременно средством эксперимента и объектом эксперимента , заменяющим изучаемый объект .
Моделирование , в-третьих, это перенос полученных на модели сведений на оригинал или, иначе, приписывание свойств модели оригиналу. Чтобы такой перенос был оправдан, между моделью и оригиналом должно быть сходство, подобие .
Подобие может быть физическим, геометрическим, структурным, функциональным и т. д. Степень подобия может быть разной - от тождества во всех аспектах до сходства только в главном. Очевидно, модели не должны воспроизводить полностью все стороны изучаемых объектов. Достижение абсолютной одинаковости сводит моделирование к натурному эксперименту, о возможности или целесообразности которого было уже сказано.
Остановимся на основных целях моделирования .
Прогноз - оценка поведения системы при некотором сочетании ее управляемых и неуправляемых параметров. Прогноз - главная цель моделирования .
Объяснение и лучшее понимание объектов . Здесь чаще других встречаются задачи оптимизации и анализа чувствительности. Оптимизация - это точное определение такого сочетания факторов и их величин, при котором обеспечиваются наилучший показатель качества системы, наилучшее по какому-либо критерию достижение цели моделируемой системой. Анализ чувствительности - выявление из большого числа факторов тех, которые в наибольшей степени влияют на функционирование моделируемой системы. Исходными данными при этом являются результаты экспериментов с моделью.
Часто модель создается для применения в качестве средства обучения : модели-тренажеры, стенды, учения, деловые игры и т. п.
Моделирование как метод познания применялось человечеством - осознанно или интуитивно - всегда. На стенах древних храмов предков южно-американских индейцев обнаружены графические модели мироздания. Учение о моделировании возникло в средние века. Выдающаяся роль в этом принадлежит Леонардо да Винчи (1452-1519).
Гениальный полководец А. В. Суворов перед атакой крепости Измаил тренировал солдат на модели измаильской крепостной стены, построенной специально в тылу.
Наш знаменитый механик-самоучка И. П. Кулибин (1735-1818) создал модель одноарочного деревянного моста через р. Неву, а также ряд металлических моделей мостов. Они были полностью технически обоснованы и получили высокую оценку российскими академиками Л. Эйлером и Д. Бернулли. К сожалению, ни один из этих мостов не был построен.
Огромный вклад в укрепление обороноспособности нашей страны внесли работы по моделированию взрыва - генерал-инженер Н. Л. Кирпичев, моделированию в авиастроении - М. В. Келдыш, С. В. Ильюшин, А. Н. Туполев и др., моделированию ядерного взрыва - И. В. Курчатов, А.Д. Сахаров, Ю. Б. Харитон и др.
Широко известны работы Н. Н. Моисеева по моделированию систем управления. В частности, для проверки одного нового метода математического моделирования была создана математическая модель Синопского сражения - последнего сражения эпохи парусного флота. В 1833 году адмирал П. С. Нахимов разгромил главные силы турецкого флота. Моделирование на вычислительной машине показало, что Нахимов действовал практически безошибочно. Он настолько верно расставил свои корабли и нанес первый удар, что единственное спасение турок было отступление. Иного выхода у них не было. Они не отступили и были разгромлены.
Сложность и громоздкость технических объектов, которые могут изучаться методами моделирования, практически неограниченны. В последние годы все крупные сооружения исследовались на моделях - плотины, каналы, Братская и Красноярская ГЭС, системы дальних электропередач, образцы военных систем и др. объекты.
Поучительный пример недооценки моделирования - гибель английского броненосца "Кэптен" в 1870 году. В стремлении еще больше увеличить свое тогдашнее морское могущество и подкрепить империалистические устремления в Англии был разработан суперброненосец "Кэптен". В него было вложено все, что нужно для "верховной власти" на море: тяжелая артиллерия во вращающихся башнях, мощная бортовая броня, усиленное парусное оснащение и очень низкими бортами - для меньшей уязвимости от снарядов противника. Консультант инженер Рид построил математическую модель устойчивости "Кэптена" и показал, что даже при незначительном ветре и волнении ему грозит опрокидывание. Но лорды Адмиралтейства настояли на строительстве корабля. На первом же учении после спуска на воду налетевший шквал перевернул броненосец. Погибли 523 моряка. В Лондоне на стене одного из соборов прикреплена бронзовая плита, напоминающая об этом событии и, добавим мы, о тупоумии самоуверенных лордов Британского Адмиралтейства, пренебрегших результатами моделирования.
1.2. Классификация моделей и моделирования
Каждая модель создается для конкретной цели и, следовательно, уникальна. Однако наличие общих черт позволяет сгруппировать все их многообразие в отдельные классы, что облегчает их разработку и изучение. В теории рассматривается много признаков классификации, и их количество не установилось. Тем не менее, наиболее актуальны следующие признаки классификации :
- характер моделируемой стороны объекта;
- характер процессов, протекающих в объекте;
- способ реализации модели.
Предварительные замечания.
Рассмотрим
многомерную систему автоматического
управления, где в качестве регулятора
используется БЦВМ, связанная с непрерывным
объектом с помощью ЦАП и АЦП (рис.1.4).
Будем считать, что измеряемый векторный
выход объектаквантуется с помощью АЦП в моментытак, что на входе БЦВМ действует векторная
решётчатая функция![]() .
В БЦВМ реализуется определённый алгоритм
управления и на её выходе формируется
последовательность дискретных значений
управляющих воздействий,
которую также можно рассматривать как
векторную решётчатую функцию. Здесь
для простоты положим, что разрядность
ЦАП и АЦП достаточно высока, так что
эффектом квантования по уровню можно
пренебречь.
.
В БЦВМ реализуется определённый алгоритм
управления и на её выходе формируется
последовательность дискретных значений
управляющих воздействий,
которую также можно рассматривать как
векторную решётчатую функцию. Здесь
для простоты положим, что разрядность
ЦАП и АЦП достаточно высока, так что
эффектом квантования по уровню можно
пренебречь.
Пусть непрерывный объект представляется дифференциальными уравнениями в форме Коши
 (2.4.1)
(2.4.1)
где –числовые матрицы соответствующих размеров.
Будем считать, что ЦАП и АЦП работают синхронно (с одинаковым периодом), но не синфазно, и пусть выдача рассчитанных управлений производится с задержкой на, где–относительное запаздывание, так что на ЦАП поступает смещённая решётчатая функция. Таким образом, эквивалентная схема принимает вид рис.2.5.

Рис. 2.5.
Очевидно, что непрерывный объект управления (2.4.1) совместно с ЦАП, АЦП и звеном задержки можно рассматривать как некоторую эквивалентную дискретную систему, на входе и выходе которой действуют решётчатые функцииисоответственно. Как и в случае импульсных систем, разностные уравнения, описывающие эту систему, должны быть такими, чтобы их решения относительно переменных выхода и состояний совпадали прис соответствующими непрерывными функциями. Эти разностные уравнения как раз и будут являться дискретной моделью непрерывного объекта в системе управления с БЦВМ в контуре. Причём, эта модель, очевидно, будет зависеть от способа восстановления непрерывного процессапо его дискретам.Применение экстраполяции нулевого порядка. Пусть операция ЦА-преобразования сопровождается формированием управленияметодом фиксации на период (экстраполяция нулевого порядка). Тогда функциябудет кусочно-постоянной (рис.2.6), удовлетворяющей условию
Для определения дискретной модели
объекта (2.4.1) при условии (2.4.2) рассмотрим
-ый
интервал дискретности![]() .
.

Рис. 2.6.
В соответствии с рис.2.6, этот интервал можно разбить на два под-интервала. На первом подинтервале, когда
Преобразуем это выражение, используя
для первого интеграла замену ![]() ,
а для второго –
,
а для второго –![]() .
Тогда после преобразований и перехода
к решётчатым функциям получим
.
Тогда после преобразований и перехода
к решётчатым функциям получим
Обозначим
и учтём, что квантование выхода производится в моменты. Тогда окончательно, искомая дискретная модель примет вид
 . (2.4.4)
. (2.4.4)
Анализируя формулы (2.4.3), заметим, что матрицы изависят от величины запаздывания. Так, если(запаздывание отсутствует), тои мы получим дискретную модель непрерывного объекта без запаздывания. Если же, то, и тогда уравнения (2.4.4) будут представлять дискретную модель с "чистым" запаздыванием на один такт.
Отметим также, что при
разностные уравнения (2.4.4) формально не
являются уравнениями в форме Коши, так
как в правой части первого уравнения
присутствует переменная, сдвинутая на
один такт по отношению к другим. Для
устранения этого "недостатка"
введем вектор дополнительных состояний
![]() ,
.
Тогда нетрудно показать, что расширенная
дискретная модель с вектором состояний
,
представится в следующем эквивалентном
виде
,
.
Тогда нетрудно показать, что расширенная
дискретная модель с вектором состояний
,
представится в следующем эквивалентном
виде
 (2.4.5)
(2.4.5)
где - новый вектор измеряемых переменных объекта, расширенных за счет управлений из предыдущего такта.
Таким образом наличие запаздывания привело к увеличению размерности дискретной модели по сравнению с размерностью непрерывного объекта. Это позволяет учесть запаздывание при синтезе алгоритмов работы БЦВМ (дискретных регуляторов), так как формально уравнения (2.4.5) представляют дискретную модель объекта без запаздывания, но повышенной размерности.
Применение экстраполяторов
-го
порядка.
При
рассмотрении этого вопроса для простоты
ограничимся случаем .
Кроме того, также для простоты, будем
считать, что управлениеявляется скалярным ().
Тогда, если для реализации этого
управления используется метод
экстраполяции-го
порядка, то на интервале![]() управлениебудет определяться выражением (1.4.10), то
есть
управлениебудет определяться выражением (1.4.10), то
есть
 , (2.4.6)
, (2.4.6)
где производные () могут быть вычислены по дискретам,в соответствии с алгоритмом (1.4.16).
Переходя к определению дискретной модели непрерывного объекта (2.4.1) запишем состояние этого объекта в конце-го интервала дискретности по известному состояниюв начале интервала. Используя формулу Коши, будем иметь
 .
.
Подставляя (2.4.6) и производя замену
![]() ,
после преобразований и перехода к
решетчатым функциям, получим
,
после преобразований и перехода к
решетчатым функциям, получим
Здесь учтено, что значения производных остаются постоянными в течение каждого интервала дискретности. Обозначим
, ,
, .
.
Тогда (2.4.7) примет вид
 .
.
Введем матрицу . Тогда, если использовать обозначение (1.4.12) для вектора, получим
где - определяется выражением (1.4.14), а- обозначает-мерный вектор (1.4.12), составленный из дискрет.
Обозначим столбцы матрицы через. Тогда учитывая структуру вектора, окончательно получим искомую дискретную модель
 . (2.4.9)
. (2.4.9)
Заметим, что несмотря на то, что по предположению управляющее воздействие формируется без задержки по отношению к моментам съема информации, дискретная модель (2.4.9) содержит запаздывания по управлению натактов одновременно. Как уже отмечалось в разделе 1.4, этот факт обусловлен использованием для формирования управленияэкстраполяции-го порядка.
Запишем полученную модель в эквивалентной форме с помощью расширенного состояния. Для этого введем вспомогательные переменные
Очевидно, что в этом случае
Тогда, если ввести вектор расширенного состояния
а также новый вектор измеряемых переменных
расширенный за счет управлений из предыдущих тактов, то (2.4.9) можно представить в следующем эквивалентном виде
 , (2.4.10)
, (2.4.10)
где
,,- матрицы размеров![]() ,,
,,![]() соответственно, имеющие следующую
блочную структуру
соответственно, имеющие следующую
блочную структуру
 ,
,
,
, .
(2.4.11)
.
(2.4.11)
Уравнения (2.4.10) представляют дискретную модель непрерывного объекта в системе управления с БЦВМ и экстраполятором -го порядка. Эта модель составлена для скалярного управления, и учет экстраполятора привел к тому, что ее размерность увеличилась напо сравнению с размерностью непрерывного объекта. Очевидно, что если рассматривать случай векторного управления, то формально дискретная модель (2.4.10) останется без изменения, но вводимые дополнительные переменныестанут векторными и общая размерность модели составит.